Step Functions Floor

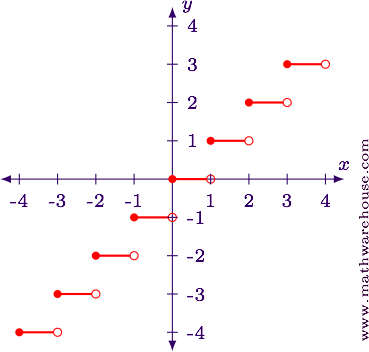
The floor function a solid dot means including and an open dot means not including.

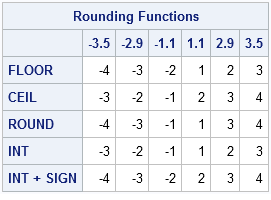
Step functions floor. The greatest integer function is often represented as x with. In mathematics and computer science the floor function is the function that takes as input a real number x displaystyle x and gives as output the greatest integer less than or equal to x displaystyle x denoted floor x displaystyle operatorname floor x or x displaystyle lfloor x rfloor. Starting with visual basic 15 8 the performance of double to integer conversion is optimized if you pass the value returned by the floor method to the any of the integral conversion functions or if the double value returned by floor is automatically converted to an integer with option strict set to off. In mathematics a common example used to introduce step functions is the greatest integer function also called the floor function.

This optimization allows code to run. Rounds downs the nearest integer. Special step functions in a floor function all non integers are rounded down to the nearest integer. Learn how to graph step functions also known as the greatest integer function in this free math video tutorial by mario s math tutoring.

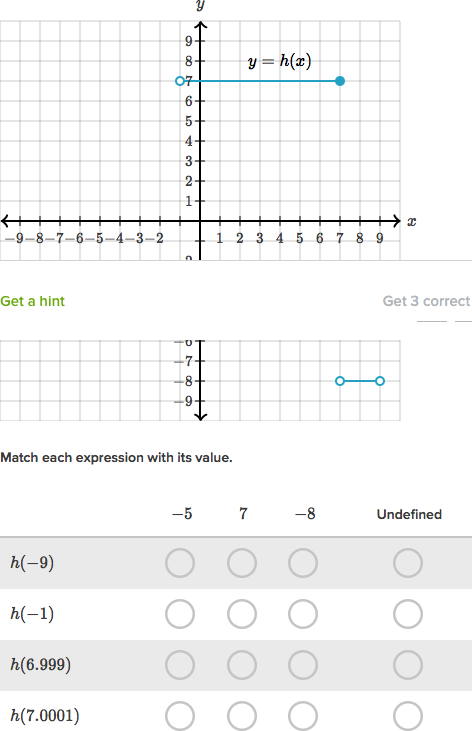
Given the graph of a step function find the function s outputs for given specific inputs. In mathematics a function on the real numbers is called a step function or staircase function if it can be written as a finite linear combination of indicator functions of intervals. The floor function is this curious step function like an infinite staircase. By using this website you agree to our cookie policy.

Returns the largest integer that is smaller than or equal to x i e. In mathematics and computer science the floor and ceiling functions map a real number to the greatest preceding or the least succeeding integer respectively. Informally speaking a step function is a piecewise constant function having only finitely many pieces. We go through some.

The way we usually count our age is an example of a floor function since we round our age down to the nearest year and do not add a year to our age until we have passed our birthday.